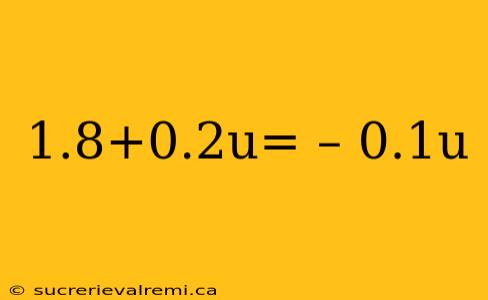Solving the Linear Equation: 1.8 + 0.2u = -0.1u
This article explores the solution to the linear equation 1.8 + 0.2u = -0.1u, providing a step-by-step solution, discussing the underlying mathematical concepts, and offering practical applications and extensions. We'll also delve into how this type of equation is used in various fields. While this specific equation might seem simple, understanding its solution lays the groundwork for tackling more complex linear equations and systems of equations.
Understanding Linear Equations
A linear equation is an algebraic equation where each term is either a constant or the product of a constant and a single variable raised to the power of one. The general form of a linear equation in one variable is:
ax + b = 0
where 'a' and 'b' are constants, and 'x' is the variable. Our equation, 1.8 + 0.2u = -0.1u, fits this format. Solving for 'u' means finding the value of 'u' that makes the equation true.
Step-by-Step Solution
Our goal is to isolate the variable 'u' on one side of the equation. Here's how we can do it:
-
Combine like terms: We have two terms with 'u': 0.2u and -0.1u. Add 0.1u to both sides of the equation to move the -0.1u term to the left side:
1.8 + 0.2u + 0.1u = -0.1u + 0.1u
This simplifies to:
1.8 + 0.3u = 0
-
Isolate the term with 'u': Subtract 1.8 from both sides of the equation:
1.8 + 0.3u - 1.8 = 0 - 1.8
This simplifies to:
0.3u = -1.8
-
Solve for 'u': Divide both sides of the equation by 0.3:
0.3u / 0.3 = -1.8 / 0.3
This gives us the solution:
u = -6
Verification
To verify our solution, we substitute u = -6 back into the original equation:
1.8 + 0.2(-6) = -0.1(-6)
1.8 - 1.2 = 0.6
0.6 = 0.6
The equation holds true, confirming that our solution, u = -6, is correct.
Applications of Linear Equations
Linear equations are fundamental tools in various fields:
-
Physics: Calculating velocity, acceleration, and displacement using equations of motion often involves solving linear equations. For example, if you know the initial velocity, acceleration, and time, you can use a linear equation to find the final velocity.
-
Engineering: Linear equations are crucial in structural analysis, circuit design, and many other engineering disciplines. For instance, calculating the forces acting on a beam or determining the current in an electrical circuit involves setting up and solving linear equations.
-
Economics: Linear equations model supply and demand relationships, cost functions, and profit calculations. Understanding the break-even point (where revenue equals cost) requires solving a linear equation.
-
Chemistry: Stoichiometry, which deals with the quantitative relationships between reactants and products in chemical reactions, heavily relies on solving linear equations.
Extensions and Related Concepts
This simple linear equation provides a foundation for understanding more complex concepts:
-
Systems of Linear Equations: Instead of one equation with one variable, we can have multiple equations with multiple variables. Solving these systems requires techniques like substitution, elimination, or matrix methods.
-
Linear Inequalities: Instead of an equals sign, we might have inequality symbols (>, <, ≥, ≤). The solution then becomes a range of values rather than a single value.
-
Graphing Linear Equations: The equation 1.8 + 0.2u = -0.1u can be graphed as a line on a Cartesian coordinate system. The x-intercept represents the solution to the equation.
Further Exploration
While this article focused on the specific solution of 1.8 + 0.2u = -0.1u, exploring online resources like Khan Academy, Wolfram Alpha, or searching "solving linear equations" on Sciencedirect will provide a more extensive understanding of linear algebra and its numerous applications.
Conclusion
Solving the linear equation 1.8 + 0.2u = -0.1u is a straightforward process that demonstrates the fundamental principles of algebraic manipulation. The solution, u = -6, is obtained by combining like terms, isolating the variable, and performing arithmetic operations. The understanding of such equations is crucial across many scientific and engineering disciplines, paving the way for more complex mathematical modeling and problem-solving. Remember that practicing different linear equations is key to mastering this fundamental concept.